コレクション ダイヤモン�� 構造 因子 638513-ダイヤモ���ド 構造因子

Isc Meiji Ac Jp

 結晶構造因子 消滅測は 結晶構造因子 から導かれます。 このとき は 番目の原子の 原子散乱因子 です。 これは原子の電子密度の分布を表しています。 つまりその原子にどれだけ電子が詰まっているかを表しています。 また、 は 番目の原子の座標を表しています。 消滅測を考えるときは、この 結晶構造因子が0 のとき の面指数 がどうなればよいかを考えます。 体心立方格子の消滅測 このように、ダイヤモンド型構造は、8つの角に全て1/8個ずつの原子が入っています。 このように1/8×8で頂点には合計1個 このように、面の中心に1/2個が6個で合計3個 ダイヤモンド型構造の単位格子の内部に4個。 よって、合計134=8個です。 これさえわかれば、ダイヤモンド型構造の質量は、 単位格子の体積cm3(単位格子) これは、簡単です。 単位格子aの3乗ですね。 単位格子

ダイヤモンド 構造因子

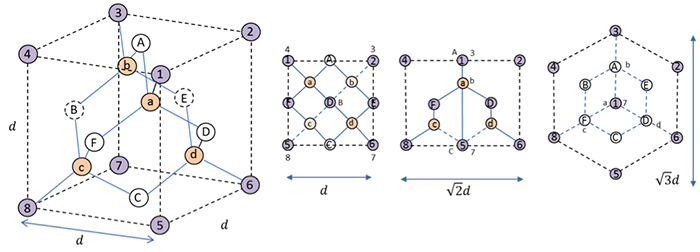
ダイヤモンド 構造因子-単位構造 ＝ 格子点に付属する原子や原子団及び分子（例：金属の結晶では原子、ベンゼンの結晶 ではベンゼン分子） 単位格子(unit cell) とは、空間格子のくり返し単位となる平行六面体のことであり、一 まず、ダイヤモンド型構造は、単位格子の1辺1辺の中点を結んでいくと、8分割出来ます。 これを、 8分割してこの8つの部屋に1つおきで原子を放り込んでいきます。 また、8分割されたとこを見てみると、このように下のようになります。 この部分を見ると、正四面体構造を表します。 この正四面体構造はこの後非常に重要になってきます！ それではまず、具体的にダイヤモンド型構

最大91 Offクーポン ベビーカーフック バギーフック 2個セット 360度回転 耐荷重 荷物 マルチ おしゃれ kg シンプル Cisama Sc Gov Br

イヤモンド構造，閃亜鉛鉱構造，ウルツ鉱構造が主な結晶構造となる． (1) ダイヤモンド 構造（Diamond Structure） 面心立方格子を一つの単位とみなし（これを単位胞と呼ぶ）， 立方体の相隣る三つの辺を x ， y ， z 軸に取り ，1 辺の長さを格 子定数 a とし六方最密構造（hcp hexagonal closedpacked) 体心立方格子(bcc body centered cubic) ダイヤモンド構造 最密充填構造 配位数＝12 最密充填構造 配位数＝12 配位数＝8 配位数＝4 sp3 混成軌道の4ボンドの制約下で最密充填 最近接原子距離 = 第2最近接原子距離 = a 結晶構造を知ってその構造因子を求める過程で消滅則が明らかとなり出現する回折ピークのミラー指数が得られます。 塩化ナトリウムは (0 0 0)に原点を持つ面心立方格子の塩素と (1/2 1/2 1/2)に原点を持つ面心立方格子のナトリウムを重ね合わせた構造である。 ダイヤモンドは (0 0 0)に原点を持つ炭素の面心立方格子と (1/4 1/4 1/4)に原点をもつ炭素の面心立方格子とを重ね合わ

ダイヤモンド構造は、（図1）のよう な、2組の同じ原子からできた面心立方格子（fcc）を対角線長の1／4だけずらした 構造となっている。 また、ダイヤモンド構造は他の構造に比べて隙間が多い。 結晶格子 点に球状の原子が互いに接して結晶を構成するとき、単位格子内で原子の占める割合 （充填率）は34%であり、面心立方格子（fcc）や六方最密構造（hcp）のような最密構 造の充填利率ダイヤモンドは結晶の方位によって硬さが著しく異 なるこ の硬度の異方性はダイヤモンドの結晶構造か ら定性的に説明することが可能である ダイヤモンド単結晶でよく見られる面は{111}, {100},{110}の3つ であるBrookesら12)は それぞ ダイアモンド格子はこの座標に (1/4,1/4,1/4)を加えた位置に同種原子を置くことで構成されます．そこで (1/4,1/4,1/4)をベクトルdと書くことにすると，追加した原子の位置ベクトルはdri (i=14)．したがって，逆格子ベクトルをGとして構造因子は S = f Σ i=14 { e^ {2πi G・ri} e^ {2πi G・ (dri)} = f (1 e^ {2πi G・d} ) (Σ i=14 e^ {2πi G・ri}) = (1 e^ {2πi・ (hkl)/4}) S

ダイヤモンド 構造因子のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

2	2	2
2	2	2
2	2	2
2	2	2
2	2	2
2	2	2
2	2	2
2	2	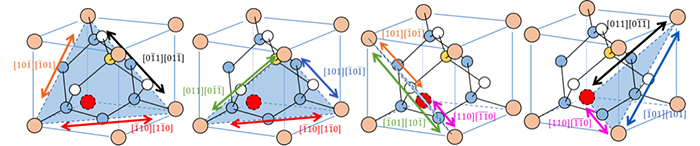2
2	2	2
2	2	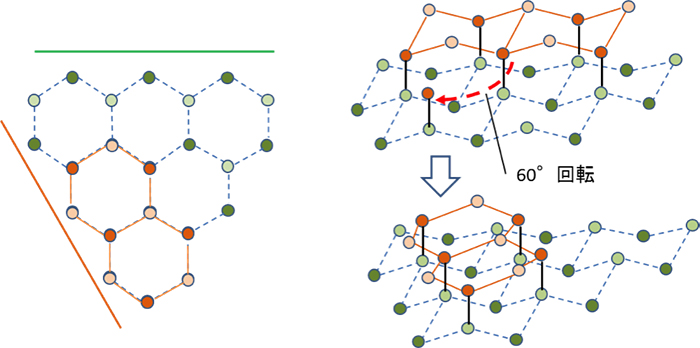2
2	2	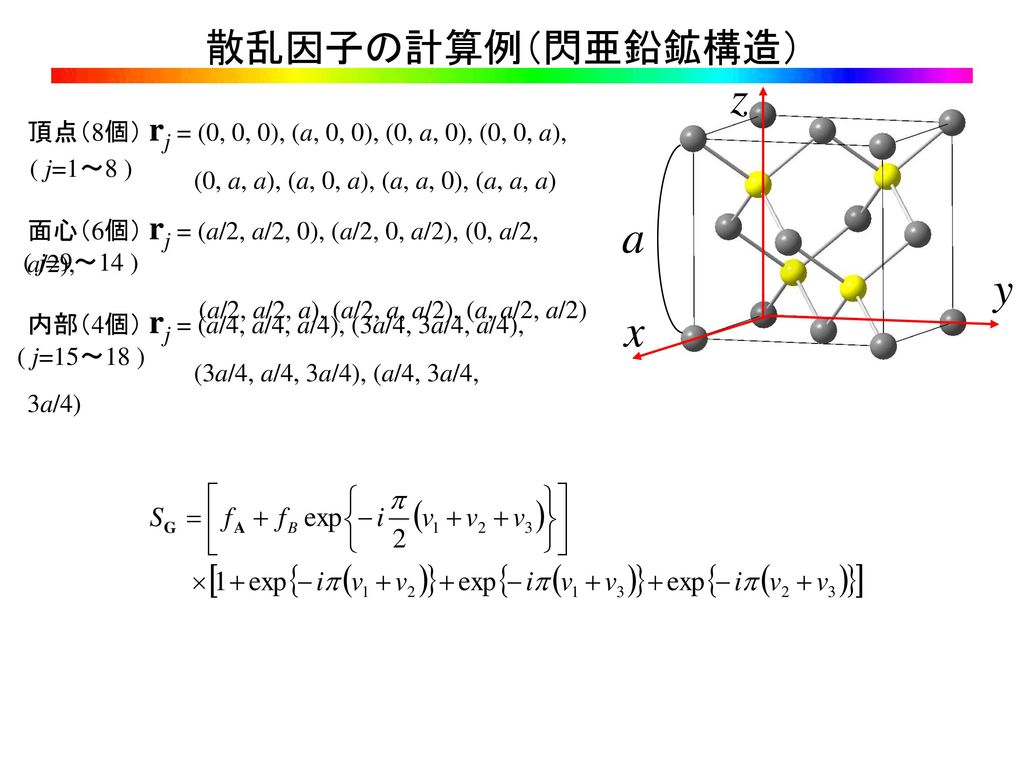2
2	2	2
2	2	2
2	2	2
2	2	2
2	2	2
2	2	2
2	2	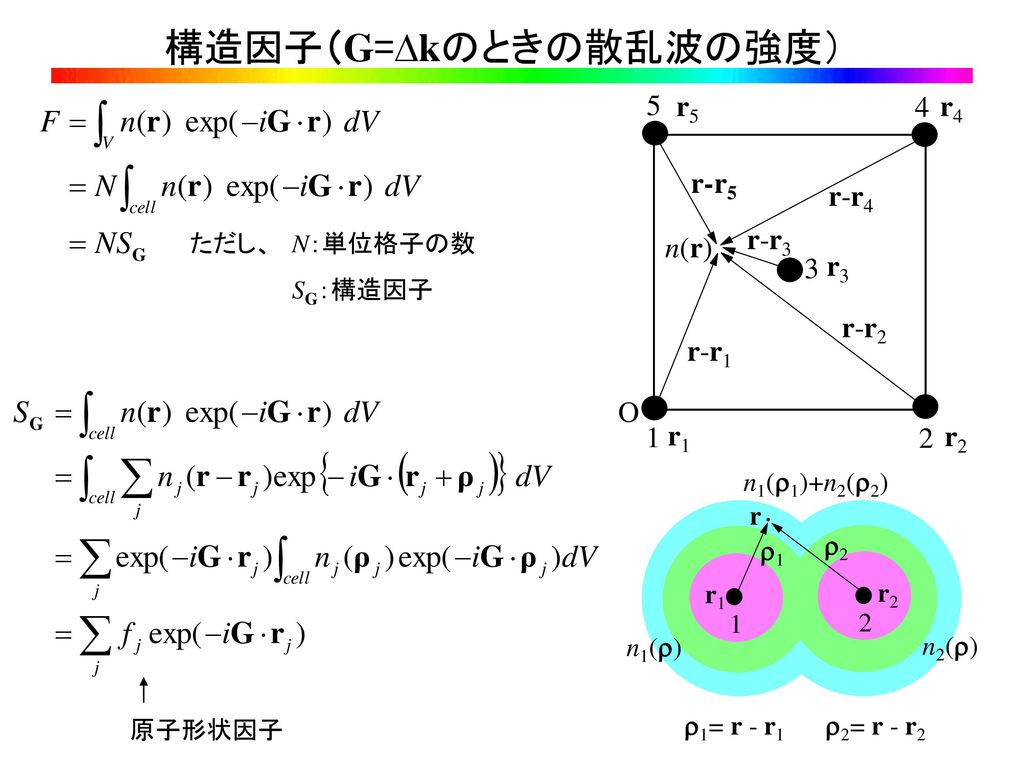2
2	2	2
2	2	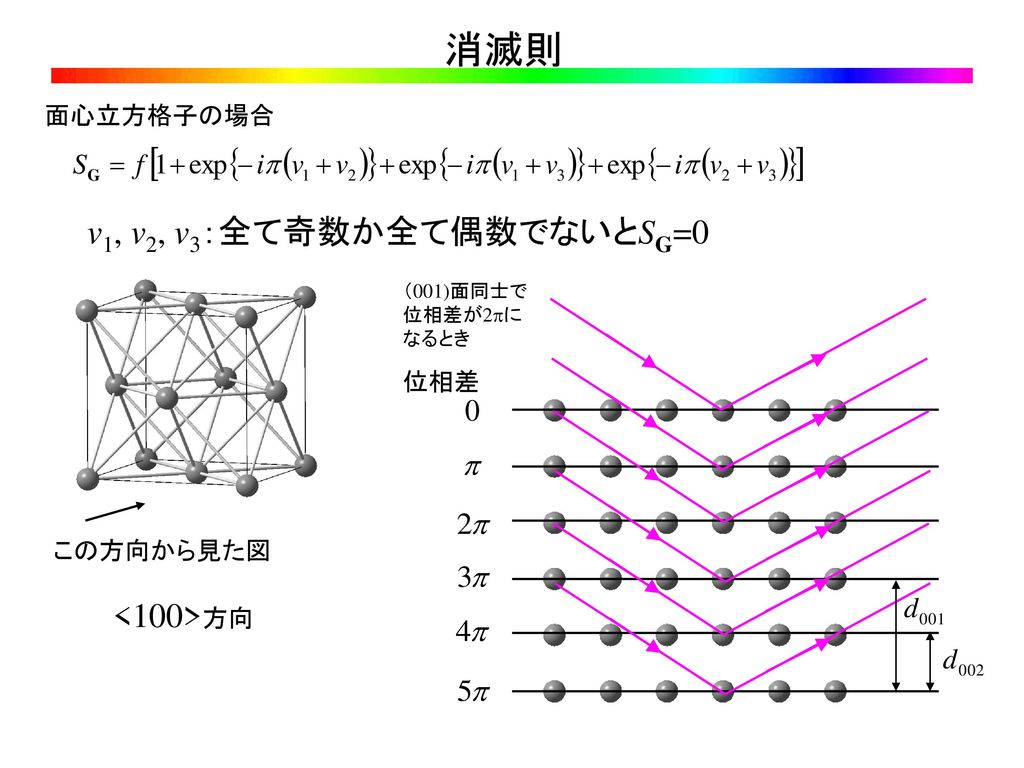2
2	2	2
2	2	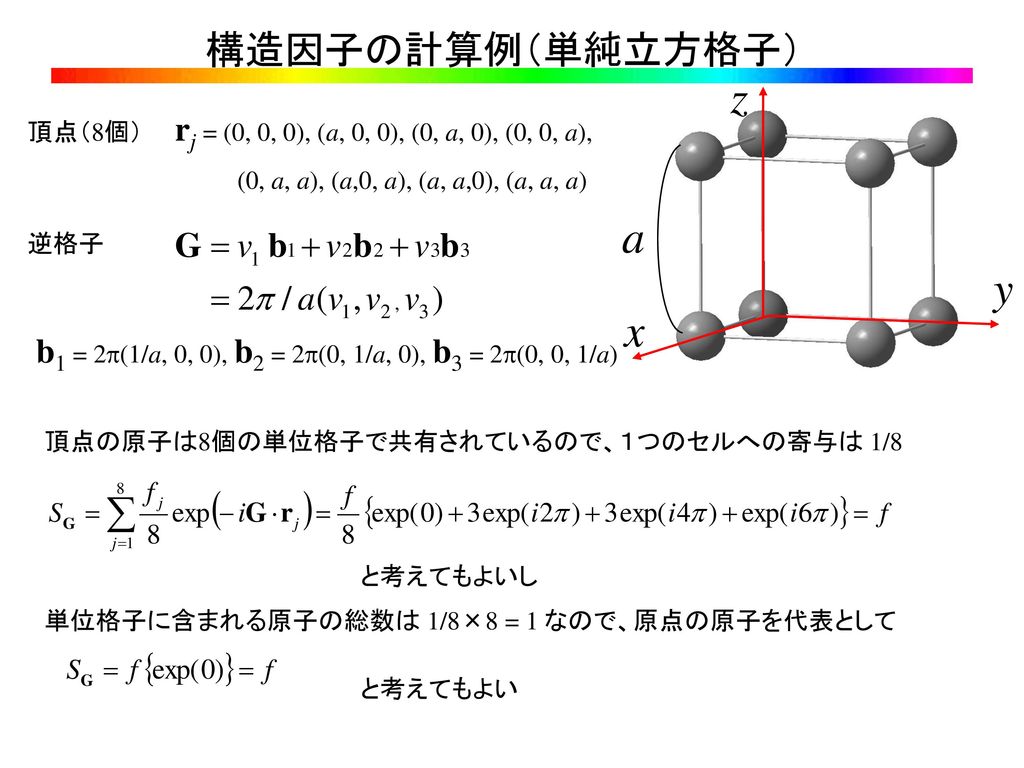2
2	2	2
2	2	2
2	2	2
2	2	2
2	2	2
2	2	2
2	2	2
2	2	2
2	2	2
2	2	2
2	2	2
2	2

 大学三年生です タイトル通りですがダイアモンドの結晶構造因子についてです。 「ダイアモンド構造をもつ半導体Siは、太陽電池やコンピューター用材料として幅広く使用されている。 Siの、111、0、400の結晶構造因子を求めよ。 Siの原子散乱因子をfsiとする」 という問題を解説と一緒にご教授願えませんでしょうか？ 自分でも考えてみたのですが、 そもそも結晶構造因子とは2 結晶構造因子の計算 結晶構造因子fは(13)式 に示したように電子密 度ρのフーリエ変換であるが,実 際の計算にこの式を 用いることはほとんどないそ れは結晶内の電子密度 は個々の原子のもつ電子密度の総和であり,原子の形

Incoming Term: ダイヤモンド 構造因子, ダイヤモンド 構造因子 計算, ダイヤモンド 構造因子 消滅則,